Work-stealing prefix scan

In my Master thesis, supervised by Prof. Paolo Bientinesi and Prof. Benjamin Berkels, I’ve had the opportunity to work on the problem of electron microscopy image registration. Instead of acquiring a single and high-quality image, which requires a long acquisition with a huge amount of energy affecting the sample, one could acquire a series of low-energy images. The images are a bit noisy, the sample is drifting while the acquisition takes place, and frames need to be registered by aligning them to a single, common coordinate system.

To align images \(f_0\) and \(f_1\), we need to find a transformation \(\phi_{0,1}\). Due to the periodical behavior of samples, we are not allowed to align any two images directly - we need to consider all subsequent steps. For example, alignment of \(f_0\) and \(f_3\) requires computing the deformations \(\phi_{0, 1}, \phi_{1, 2}\) to produce \(\phi_{0, 2}\), and estimating the transformation \(\phi_{0,3}\) using \(\phi_{0,2}\) and \(\phi_{2,3}\).

To a computer scientist, this problem is a classic example of a prefix sum (scan). In a prefix computation, a sequence of elements \(x_0, x_1, \dots, x_{n}\) is transformed to produce elements \(y_i = x_0 \odot x_1 \odot \dots \odot x_{i-1}\). Prefix sums have been studied extensively since the 60’s because binary addition is a prefix sum problem, and scan parallelizations allow to build faster binary adders. Prefix scans are considered a classic parallelism pattern - many seemingly sequential problems can be parallelized when represented as a prefix scan.

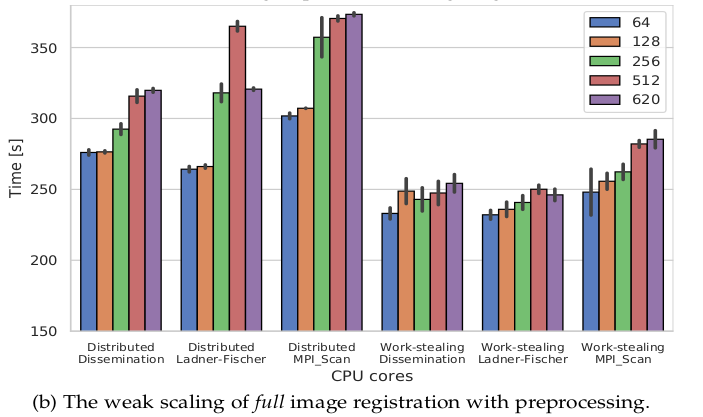
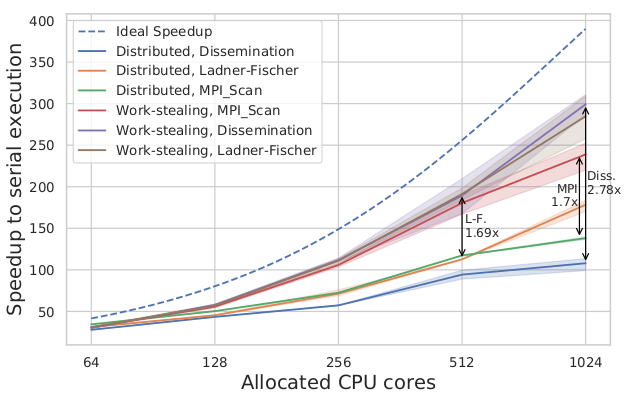
While our problem can be represented as a prefix scan, its characteristics are quite different from the scans analyzed in the literature: the image registration operator is computationally intensive and has unpredictable and highly imbalanced execution cost. In the Master thesis, I analyzed the prefix sum algorithms and their distributed implementations, and I found out that the MPI_Scan performance is unsatisfactory. The work has been presented as a poster at the Student Research Competition at SC ‘17.

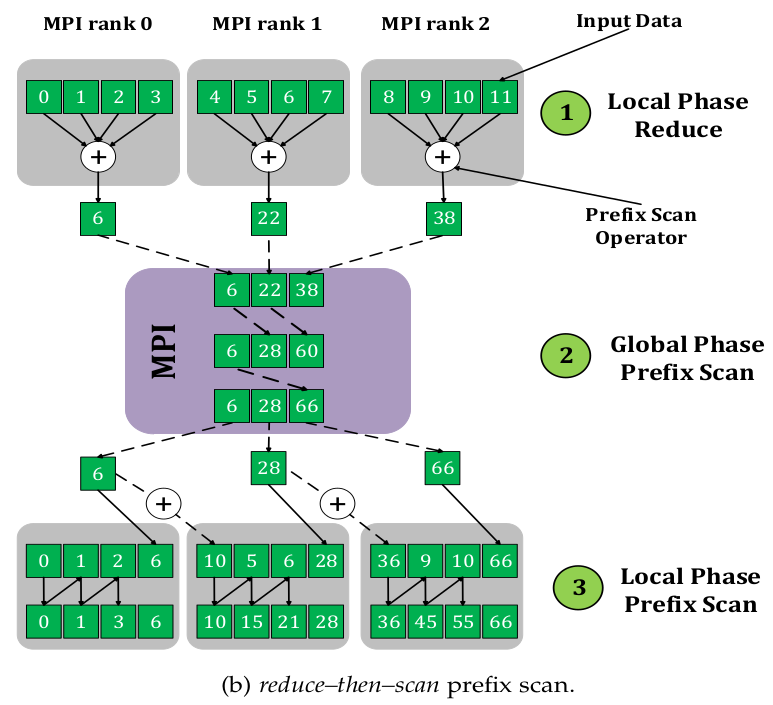
To provide a fast and efficient parallelization strategy for the image registration, we developed a novel work-stealing prefix scan algorithm to provide load balance for the tightly constrained scan algorithms. We have shown that the new approach provides up to a two-fold decrease in computation time and up to a 2.25x decrease in CPU resources and energy consumption. The research paper has been published in the IEEE Transactions on Parallel and Distributed Systems.